Qu’est-ce que le son, la fréquence d’échantillonnage et la profondeur de bit ?
Pour bien comprendre ces notions, il faut d’abord comprendre ce qu’est le son.
Voici donc une petite partie théorique. Rassurez-vous, je vais la simplifier au maximum. Il faut vraiment comprendre ces notions de base, car elles vous accompagneront dans tous vos enregistrements.
Le son est constitué de vibrations du milieu dans lequel il se propage. Comparez cela à l’onde produite par un caillou dans un lac.
Cette onde peut se propager dans l’air, dans l’eau ou dans la matière solide.
Prenons le cas du son le plus simple. Il se représente par une courbe sinusoïdale. Votre logiciel MAO peut d’ailleurs certainement produire ce type de son.
Le son pur : l’onde sinusoïdale
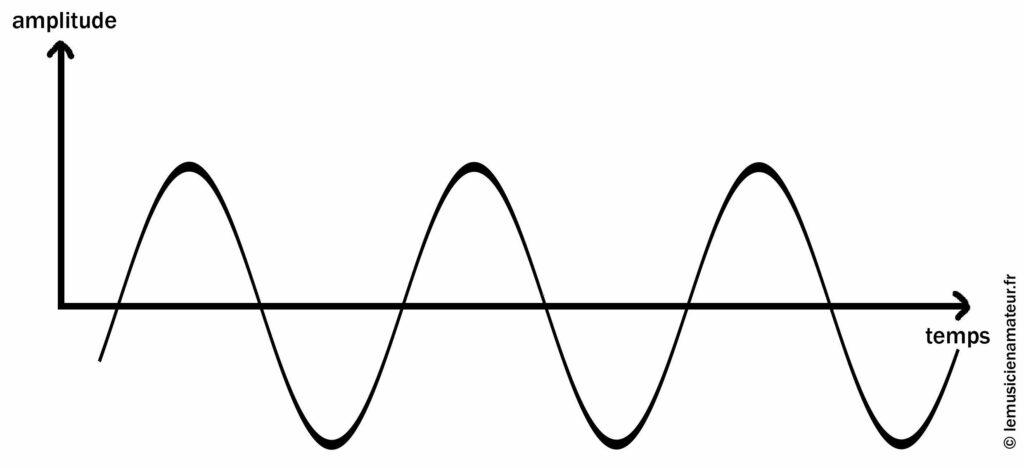
Cette courbe correspond au signal enregistré à travers votre micro et retransmis par vos enceintes lors de la lecture.
Nous allons voir 2 caractéristiques indispensables, à connaître absolument.
L’amplitude
L’amplitude est la mesure verticale sur le schéma. En effet, le signal rouge va plus loin en haut et en bas par rapport au signal noir.
L’onde rouge a donc une amplitude supérieure à l’onde noire.
Cela se caractérise à l’oreille par un signal plus fort.
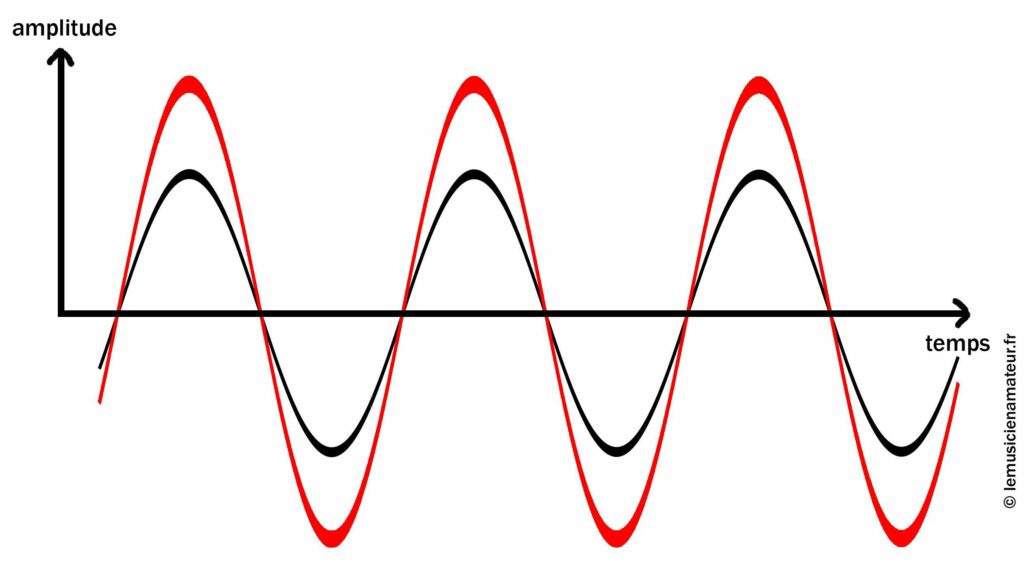
L’onde rouge a une amplitude supérieure à l’onde noire.
La période
Par définition, la période est la durée minimale qui sépare 2 événements identiques.
Dans le langage courant, une année peut être considérée comme une période, car les années se succèdent les unes aux autres de manière identique (d’un point de vue temporel).
Sur le schéma, la flèche indique la durée minimale avant que le phénomène soit répété, identique à lui-même (ici, une vague au-dessus et une en-dessous de la ligne centrale).
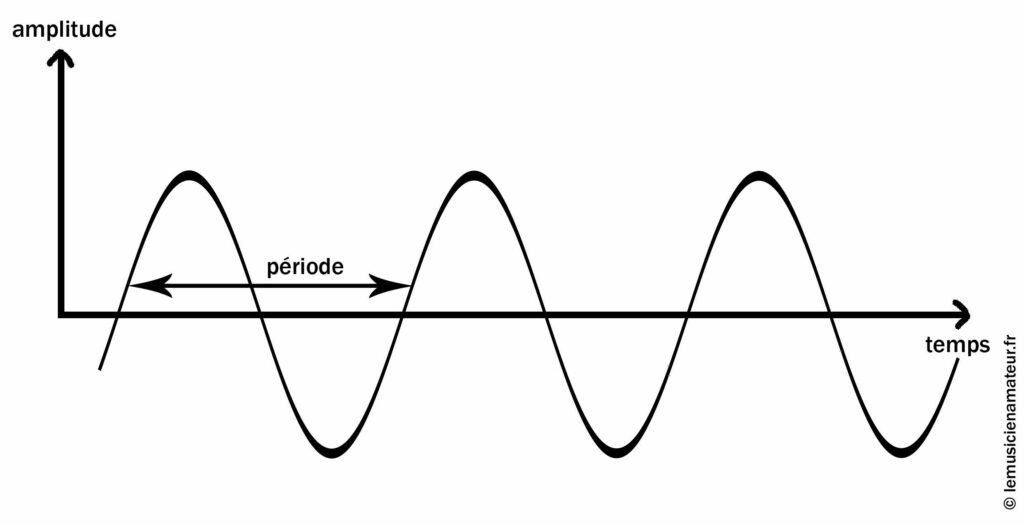
Période de l’onde sinusoïdale
Voici un second schéma avec 2 ondes avec 2 périodes différentes :
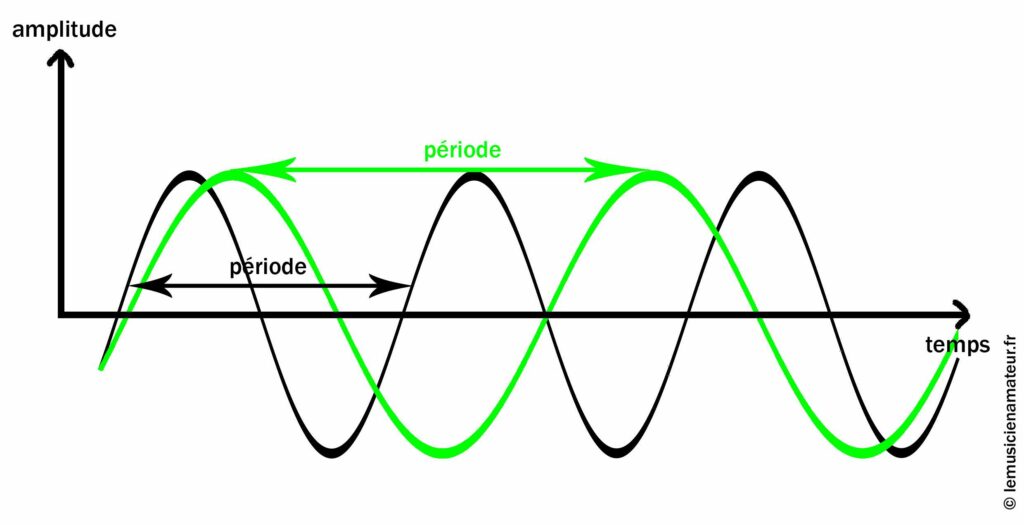
Petite remarque au passage : ces 2 ondes ont des périodes différentes, mais la même amplitude.
Comment cela va-t-il s’entendre à l’oreille ?
Nous avons vu que l’amplitude correspondait au volume sonore, mais qu’en est-il de la période ?
Hé bien vous entendrez une différence de note.
En effet, plus la période est courte, plus la note entendue sera aigue, et plus la période est longue, plus la note sera grave.
Cela dit, on utilise surtout la notion de fréquence.
La fréquence est le nombre de périodes par seconde.
Pour les matheux, on l’obtient en donnant l’inverse mathématique de la période : f = 1/T
f étant la fréquence en Hz (Hertz) et T étant la période en seconde.
Pas de panique ! Voici un exemple concret !
Prenons une guitare. La corde la correspond à une fréquence de 110 Hz.
Pour la suite, il faut connaître quelques valeurs :
- L’oreille humaine entend en général les fréquences comprises entre 20 Hz et 20 kHz (kHz = kilo Hertz, donc 20 kHz = 20 000 Hz)
- La corde mi grave d’une guitare a une fréquence d’environ 80 Hz (82,4 Hz pour les puristes)
- La corde mi grave d’une guitare basse a une fréquence d’environ 40 Hz
Pour ceux et celle qui en veulent plus :
- En théorie musicale, une octave est l’intervalle entre 2 notes de même nom (exemple : do et le do suivant)
- Monter d’une octave signifie doubler la fréquence (exemple : note la 110 Hz, le la suivant 220 Hz, le suivant 440 Hz, etc.)
- On considère les sons graves entre 20 Hz et 200 Hz, les sons médiums entre 200 Hz et 2 000 Hz, les sons aigus entre 2 000 Hz et 20 000 Hz
- En-dessous de 20 Hz, on parle d’infrasons
- Au-dessus de 20 kHz, on parle d’ultrasons
Vous voyez, finalement, ce n’est pas très compliqué. Retenez surtout l’amplitude et la fréquence car ces notions seront vitales pour la suite.
Petit exemple récapitulatif :
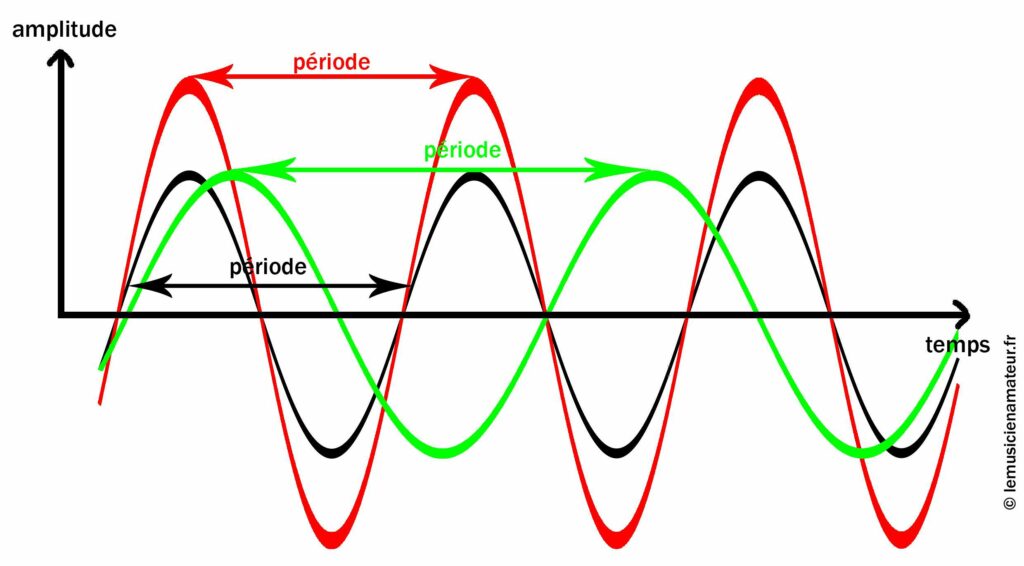
Quel sera le rendu de chaque courbe par rapport à la noire ?
- La verte sonnera plus grave que la noire, mais avec le même volume sonore
- La rouge donnera la même note que la noire, mais à volume plus fort.
Analogique / numérique
Dans notre exemple, le signal est analogique, c’est-à-dire le signal exact produit par la source sonore.
Mais votre carte son et votre ordinateur utilisent un signal numérique. Le signal sera donc transformé en une suite de 0 et de 1, signaux compréhensibles par la machine.
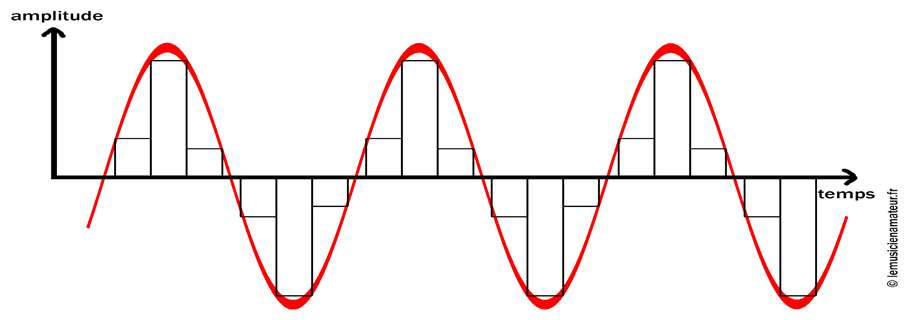
Voici le principe de transformation de la courbe analogique en signal numérique. Le but est d’avoir quelque chose le plus proche possible de la courbe d’origine.
En langage numérique, on va avoir une quelque chose de ce type :
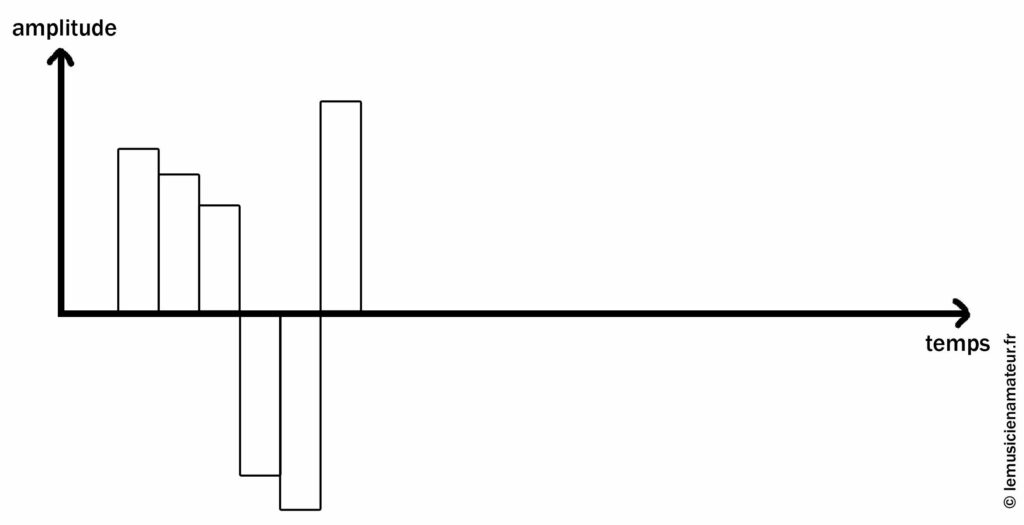
Signal numérique
Les valeurs seront donc moins précises à cause de la forme de nos rectangles.
Comme nous le disions, le but est de transformer notre courbe de départ en signal numérique.
Cela donnerait ceci :
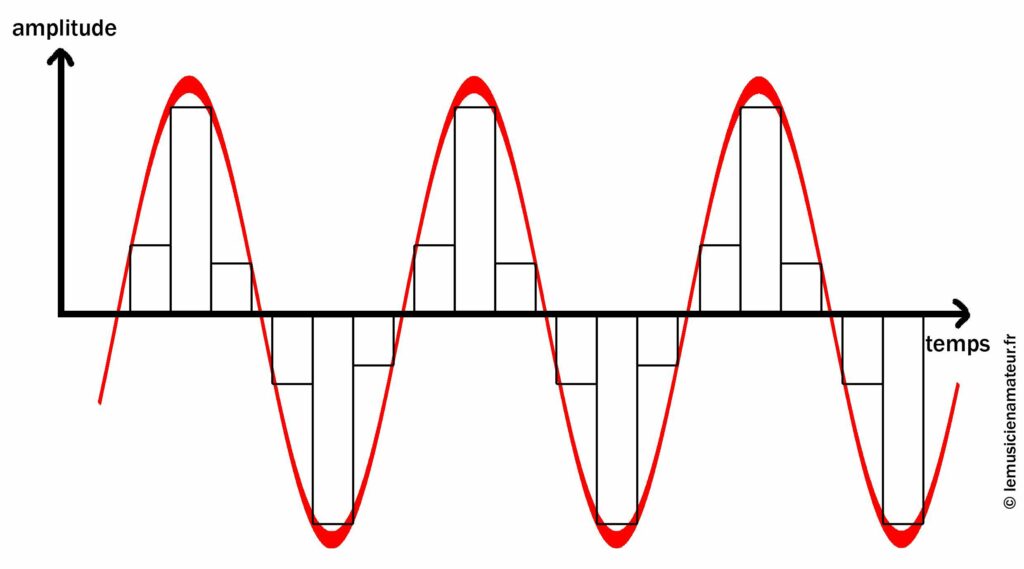
Transformation analogique/numérique
En enlevant la courbe rouge, cela donne ceci :
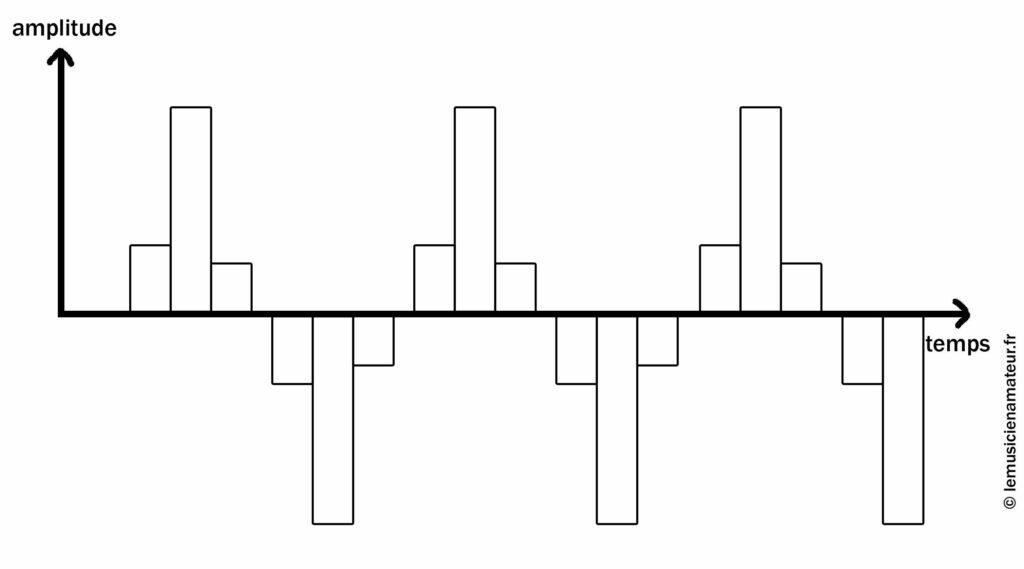
Signal numérique
Vous imaginez bien que le rendu ne sera pas terrible, étant donné le caractère approximatif de ce qu’on obtient…
Pour se rapprocher au maximum de la courbe d’origine, on va utiliser 2 notions : la fréquence d’échantillonnage et la profondeur de bit.
La fréquence d’échantillonnage
Vous allez voir, ce n’est pas compliqué. Nous allons tout d’abord utiliser des rectangles moins larges. De ce fait, il nous en faudra beaucoup plus :
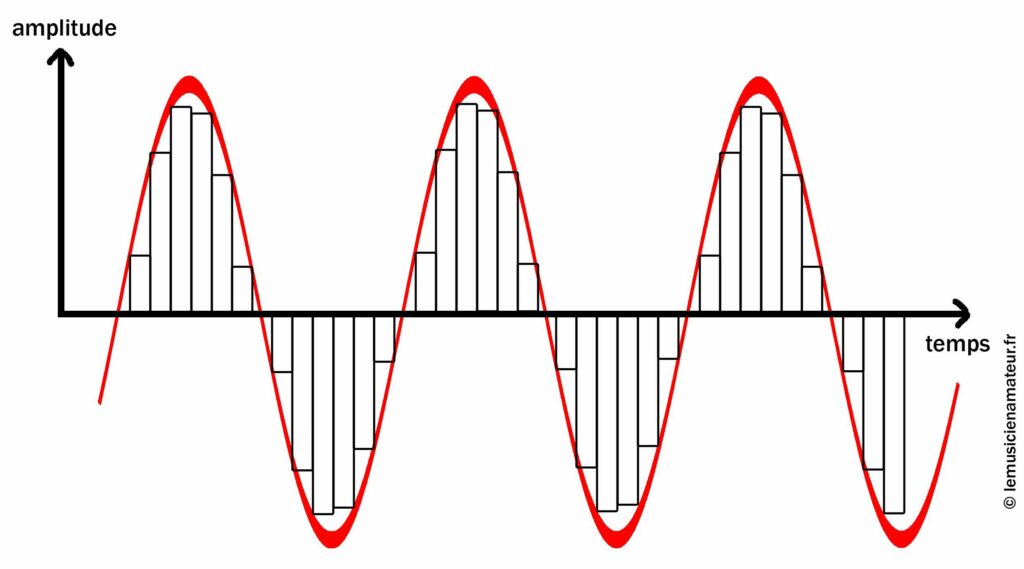
Fréquence d’échantillonnage plus importante
En enlevant le signal rouge, cela donne ceci :
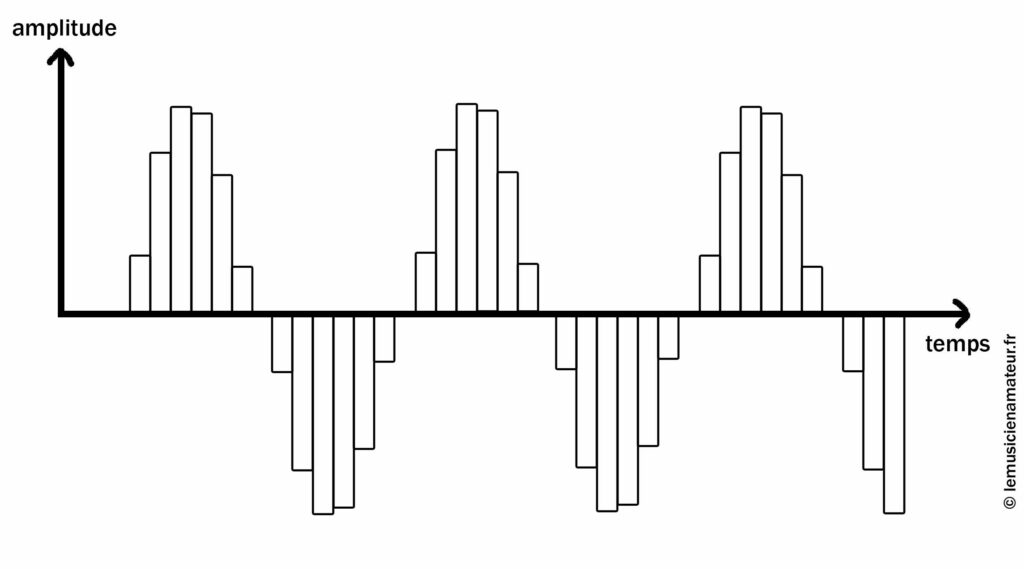
Vous voyez qu’on se rapproche de la courbe d’origine. Et plus on ajoutera de rectangles, plus le signal sera fidèle à l’original.
C’est cela qu’on appelle la fréquence d’échantillonnage !
Plus cette fréquence sera grande meilleure sera le rendu.
À titre indicatif, la fréquence d’échantillonnage d’un CD est de 44,1 kHz. En vidéo, elle est souvent de 48 kHz.
Pour ceux et celles qui en veulent plus :
Cette valeur de 44,1 kHz s’explique. Vous vous rappelez ? Nous avions vu que l’oreille humaine entendait jusqu’à 20 kHz. Or, pour avoir un son correct, la fréquence d’échantillonnage doit être le double de celle qu’on entend.
On retrouve donc bien une valeur d’environ 40 kHz. C’est le physicien Nyquist qui a mis cette norme en évidence.
La profondeur de bit
Voyons une seconde façon d’améliorer le signal. Reprenons notre courbe de départ :

Il faut prendre en compte le nombre possible de valeurs pour la taille verticale de nos rectangles.
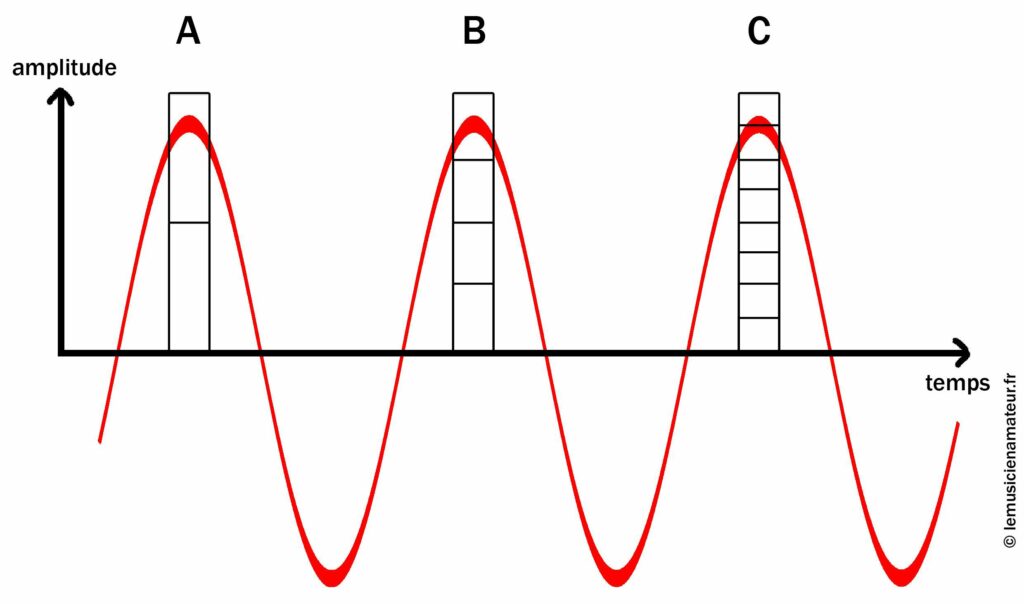
Profondeur de bit
Dans le rectangle A, nous avons uniquement 2 valeurs possibles pour nos rectangles. Même en prenons le plus proche de la courbe rouge, on se trouvera avec un signal relativement loin de la réalité.
Dans le rectangle B, nous avons 4 valeurs possibles. On imagine que le son sera mieux défini, car on se rapproche de la bonne valeur.
Dans le rectangle C, avec 8 valeurs possibles, on arrive à un résultat beaucoup plus convenable.
Donc, pour avoir le meilleur signal possible, il faut le plus de valeurs possibles. C’est ce qu’on appelle la profondeur de bit.
Plus vous avez de bits, meilleure sera votre définition.
À titre indicatif, un CD a une résolution de 16 bits.
Que devez-vous choisir dans votre logiciel MAO pour vos prises de son ?
On pourrait croire que la qualité CD est suffisante ?
Ce n’est pas faux. Cela dit, il vaut mieux passer en 24 bits. En effet, la plage dynamique est beaucoup plus grande qu’en 16 bits. Cela aura pour conséquence d’éliminer certains types de bruits lors de la conversion analogique/numérique.
Vous pourrez toujours repasser en 16 bits plus tard si vous le souhaitez, lors de l’étape du mastering.
Remarque :
Évidemment, plus vous augmentez votre fréquence d’échantillonnage et le nombre de bits, plus votre fichier audio sera gros.
Mono / stéréo
Je pense que tout le monde connaît la différence entre mono et stéréo.
En stéréo, vous avez 2 signaux distincts (droit et gauche) qui permettent un rendu plus naturel du fait que vous avez 2 oreilles.
OK, jusque-là, rien de bien neuf…
Ceci étant, prenez vraiment en considération que beaucoup de systèmes audio rendent plus ou moins en mono !
Par exemple, sur une télé, vous avez le signal droit et le signal gauche qui sont très rapprochés. Et plus vous vous en éloignez, plus vous aurez l’impression d’être en mono.
Idem pour les petits postes ou les petites enceintes bluetooth…
Il était très important de donner un peu de théorie sur les différents paramètres à régler, ainsi que leurs intérêts.
Une bonne configuration minimale serait donc de 24 bits 44,1 kHz, ou 48 kHz si la destination est la vidéo. Il est bien entendu possible d’aller plus haut si vous le désirez, mais reste à voir si c’est vraiment utile…